Application Example¶

• Índice de contenidos
• Application Example
  • Detecting normal EKG pulses.
  • About the EKG
  • Preprocessing
  • Training
  • Adding some noise
  • Selecting the right weights
  • Now what?

Detecting normal EKG pulses.¶

I will not enter into too much detail in this text in an attempt to trick the reader (you) into doing some research. But the basic idea is to train an MLP and then use the results to try and deduce if a Pulse is normal or not (the same approach can be used to detect specific pathologies).

This is not the usual approach which usually includes extracting features like the a_ks of the Fourier Transform, eigenvalues, and such. The approach that will be described in this example is much simpler (albeit it has a less accurate result... or does it?)

About the EKG¶

EKGs or ECGs (whichever you like) is basically a set of five (three, five or six) different signals or derivations. Most of the bibliographic information and cardiological knowledge is in the time domain, and unfortunately most of the features usually extracted for NN training are frequency based, which brings us to a little problem, no cardiologist wants to apply something that he/she can't understand.

We can of course analyze an ECG in the time domain, and with a little tinkering the results are actually quite encouraging.

Preprocessing¶

As you might know before throwing a signal at a NN and expecting great results is usually coherent to to some filtering and transforming I'll keep the filtering to a minimum, and mostly done in order to have nice function plots.

Let's start by getting a copy of [mrft] and some EKG Data (for convenience there are some samples included in mrft), in case you don't like them, you are free to search some, manufacture one, or even use a synthesizer like Java ECG Generator.

Training¶

Open mrft select the menu Examples->EKG (Synth) this will populate the tables the following way:

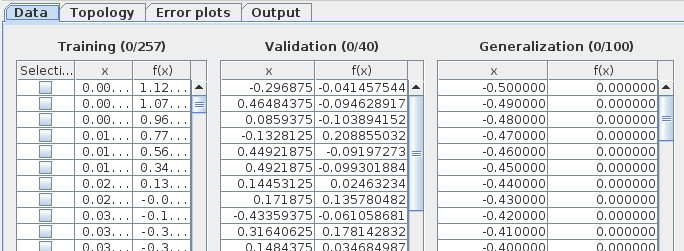
Go ahead and press F5 (a training session should start and with some luck converge to an "acceptable" fit).

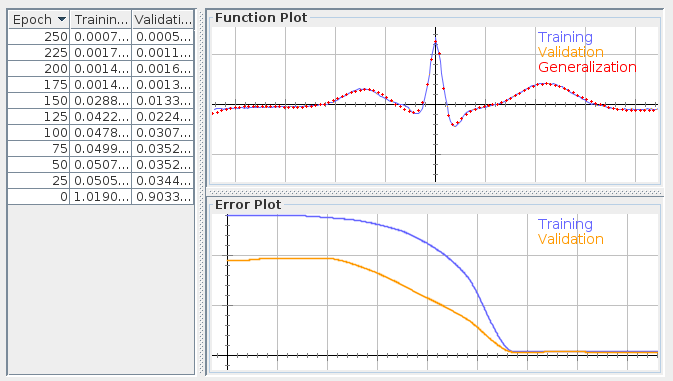
There's something odd with the way this MLP is trained... do you see it? No?

(Tip: in the lower plot both the training and validation errors stay very close together! they should be diverging, or at the very least separate, remember over-fitting?) This usually happens with synthetic data, since adjustment is too perfect the training and validation datasets are basically one in the same.

Adding some noise¶

Noise is a bad thing that should be removed, why do we want to add it? well the fact is that NN tend to work better with noisy data (not so noisy mind you).

There are several ways to add noise, but for this we'll use a transformation, so go to Dataset -> Transform... -> Custom Function (All), something like this should appear:

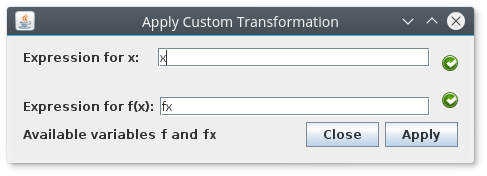
We'll leave the x value as it is, but in the fx text field write: gaussian2(fx, 0.1) then click on apply, your data now must look something like this:

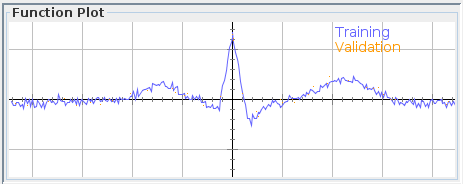
Try pressing F5 now so it re trains...

Yes, I lied (not entirely) gaussian noise didn't change the validation error, but I'll let you figure out why on your own (one clue: Box–Muller, the rest is simple math). For a bit more information about this see Adding noise in Data manipulation

Selecting the right weights¶

As the NN trains itself the synaptic weights of the training epochs are saved (not all of them), so now we must decide which of all the weights to use, click on the error table (Error Plots panel), and when you start selecting rows, you should see two things, one is that the red plot of the function plot changes, and the second one is that a line (or guide) appears in the error plot this indicates in the graph the moment of that particular weight.

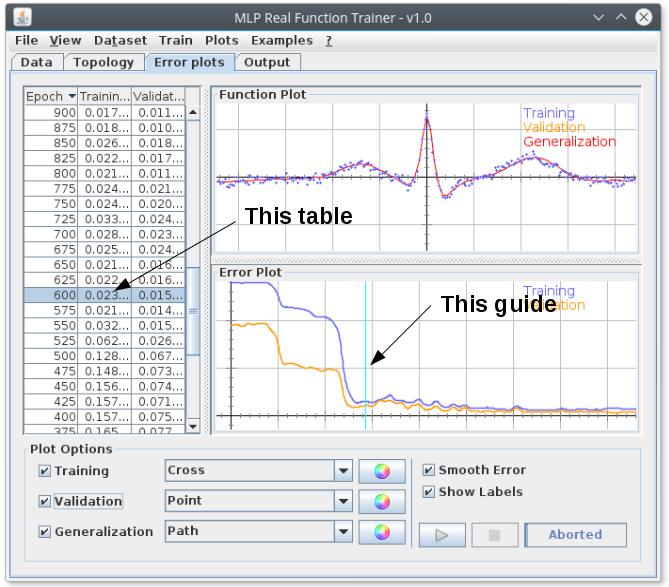
Once you are satisfied with the results (i.e. choose the "best" weights ¹)

Now what?¶

I don't actually have time to finish it today, but the gist is: we will use that synaptic weight to predict values of an unknown EKG, and estimate how similar is it with the training value (mse), with that, we'll choose the one with the lowest mse (mean square error) is the one that we'll accept as correct.
@TODO complete example

¹ There are several criteria for choosing the "best" as a rule of thumb pick the closest to the left with the lowest error, or the point where the validation an training errors intersect. ↩